Quantum Computing Primer
[TOC]
Foundation of Quantum Computing
Qubit Representation
单个量子比特(qubit)的状态可以在复数域\(\mathbb{C}\)上二维希尔伯特空间(Hilbert space)中表示, 不妨用狄拉克符号\(\vert\psi\rangle\)表示, 该符号称为右矢(ket).
希尔伯特空间是一个完备的内积空间, 由内积引申可以得到正交, 模长, 角度等概念. 在这个复数域\(\mathbb{C}\)上二维希尔伯特空间中总可以选择两个完备的正交归一基, \(\vert0\rangle\) 和 \(\vert1\rangle\) 线性表出任意一个向量\(\vert\psi \rangle\), 即\(\exists! \alpha, \beta \in \mathbb{C}, st. \vert\psi \rangle = \alpha \vert0 \rangle + \beta \vert1\rangle\). 在该组基底下, 任意矢量\(\vert\psi \rangle\)和两个基底\(\vert0\rangle\) 和 \(\vert1\rangle\) 用矩阵的方式表示为:
\[|\psi\rangle = \left(\begin{array}{c} \alpha\\ \beta \\ \end{array}\right) , |0\rangle = \left(\begin{array}{c} 1\\ 0 \\ \end{array}\right) , |1\rangle = \left(\begin{array}{c} 0\\ 1 \\ \end{array}\right)\]由于定义在复数域\(\mathbb{C}\)上, 我们很方便地可以定义一个右矢\(\vert \psi \rangle\)的共轭转置, 记为\(\langle \psi \vert\), 即\(\langle \psi \vert = {\vert \psi \rangle}^{\dagger}\). 在矩阵上表示为
\[|\psi\rangle = \left(\begin{array}{c} \alpha\\ \beta \\ \end{array}\right) , \langle\psi|=\left(\alpha^{*}, \beta^{*}\right)\]该符号被称为左矢(bar), 是因为这样可以非常美观地表示内积, 如内积\(\vert\psi \rangle \cdot \vert \phi \rangle\)可以写成\(\langle \psi \vert \phi \rangle\). 当然, 自身与自身的内积可以得到模长\(\langle \psi \vert \psi \rangle = \vert\alpha\vert^2 + \vert\beta\vert^2 \geq 0\).
在量子计算中, 但是我们并不关心全局相位的大小, 即 \(\vert\psi \rangle\)和 \(t\vert\psi \rangle (t \in \mathbb{C})\)被认为是一样的. 因此我们统一归一化规定
\[|\alpha|^2 + |\beta|^2=1\]上面的形式很容易想到进行三角化, 为了后面的形象化表示, 我们总可以通过改变全局相位的方式使得第一个分量\(\alpha\)变成实数. 故在不关心全局相位的情况下, \(\vert \psi \rangle\)可以被表示成:
\[|\psi\rangle = \cos{\frac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\frac{\theta}{2}} |1\rangle= \left(\begin{array}{c} \cos{\frac{\theta}{2}}\\ e^{i\phi}\sin{\frac{\theta}{2}}\\ \end{array}\right)\]之所以是这样表示, 是因为我们可以引入Bloch球表示量子比特, 而此时\(\theta\)和\(\phi\)在Bloch球有类似于极坐标的直观意义, 我们也可以看到此时 \(\vert0\rangle\) 和 \(\vert1\rangle\)在Bloch球上的位置.
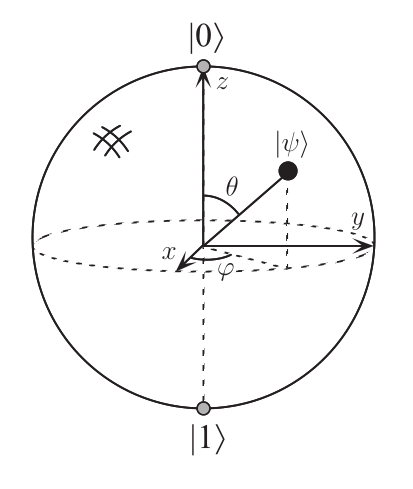
由于Bloch球只是一个直观意义, 有几个误区要指出:
- 毕竟是希尔伯特空间而不是欧几里得空间, 所以不存在\(\vert0\rangle + \vert1\rangle =0\)这种说法, 实际上\(\frac{\vert0\rangle \pm \vert1\rangle}{2}\)分别是x轴正负半轴与球面的交点, 这两个状态在后面介绍Hadamard门时会出现.
- 但是后面介绍的少部分量子门可以在bloch球上得到直观解释, 如Hadamard门相当于绕x轴与z轴的角平分线逆时针旋转180度(相当于x,z轴交换位置, y正半轴变成指向原本y负半轴的方向)
- 映射到Bloch球面的时候需要第一个分量为实数, 如\(\frac{1}{2}\left(\begin{array}{c}1+i\\ 1-i \\ \end{array}\right)\)和\(\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ -i \\ \end{array}\right)\)实际上都是表示y负半轴与球面的交点.
同时, 容易从极坐标得到\(x\), \(y\), \(z\)的表达式:
\[\begin{aligned} &x = \sin \theta \cos \phi\\ &y = \sin \theta \sin \phi\\ &z = \cos \theta \end{aligned}\]Qubit Measurement
在物理上, 任意一次测量都可以看作一个自伴算符\(O\), 即满足\(O^{\dagger}= O\). 特别地, 如果\(\lambda\)和\(\vert\psi \rangle\)满足 \(O \vert \psi \rangle = \lambda \vert \psi \rangle\), 则\(\lambda\)和\(\vert\psi \rangle\)分别称为本征值和本征态. 一次测量结果只能是本征值中一个, 且测量后量子态会坍塌到对应的的本征态.
关于自伴算符, 有如下的定理:
根据有限维的谱定理,必定存在着一个正交归一基,可以表达自伴算符为一个实值的对角矩阵.
不妨设这组正交归一基为\(\{ \vert \psi_i \rangle \}\), 则\(O\)在该组基底下的矩阵表示为\(diag\{\lambda_0, \lambda_2, \dots, \lambda_{n-1}\}(\lambda_i \in \mathbb{R})\), 显然\(\{\lambda_i\}\)和\(\{\vert\psi_i\rangle\}\)恰为本征值和本征态, 即\(O\vert\psi_i \rangle = \lambda_i \vert \psi_i \rangle\).
假设一个量子态\(\vert\psi\rangle\)在这组基下表示为\(\vert\phi \rangle = \sum\limits_{i=0}^{n-1}c_i\vert\psi_i\rangle\)(对于单个量子比特\(n=2\), 这里讨论一般情况, 后面引入多量子比特后会n增大), 由归一性易得\(\sum\limits_{i}\vert c_i\vert^2=1\).
对该量子态进行测量相当于进行一次投影. 实际上, 通过计算\(\langle \phi \vert O \vert \phi \rangle\), 我们可以求得期望值:
\[\begin{aligned} &\langle \phi | O | \phi \rangle \\ =&(\sum\limits_{i}c_i^{*}\langle \psi_i| ) O (\sum\limits_{j}c_j |\psi_j\rangle ) \\ =&(\sum\limits_{i}c_i^{*}\langle \psi_i| ) (\sum\limits_{j}c_j O |\psi_j\rangle ) \\ =&(\sum\limits_{i}c_i^{*}\langle \psi_i| ) (\sum\limits_{j}c_j \lambda_j |\psi_j\rangle ) \\ =&\sum\limits_{i,j}c_i^{*}c_j\lambda_j\delta_{i,j} \\ =&\sum\limits_{i}|c_i|^2\lambda_i \end{aligned}\]其中本征值\(\lambda_i\)的概率为\(\vert c_i\vert^2\), 期望值为\(\sum\limits_{i}\vert c_i\vert^2\lambda_i\).
同理, 我们可以得到某个本征态$\vert \phi_i \rangle$出现的概率 \(\begin{align} \vert \langle \psi_i \vert \phi \rangle \vert^2 &= \vert \langle \psi_i \vert (\sum_k c_k \vert \psi_k \rangle) \vert^2\\ &= \vert c_i \langle \psi_i \vert \psi_i \rangle \vert^2 \\ &= \vert c_i\vert^2 \end{align}\)
Single Quantum Gate
Multiple Quantum Gate
Quantum Algorithm
[To be continued…]