A Guide to Homomorphic Encryption Library SEAL

Resource

• Intro to Homomorphic Encryption, Credit to Microsoft Research

Overview

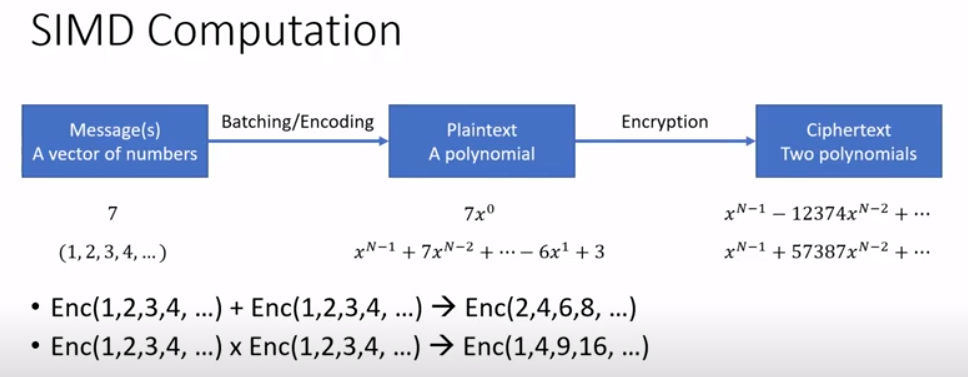
• Number of message slots: $N$ in BFV, $\frac{N}{2}$ in CKKS(in later section)

• The more message slots you have, the more parallelism you could achieved!!!

BFV Algorithm

Polynomials

BFV algorithm is manipulated on a polynomial ring $R = \mathbb{Z}[X]/(X^n+1)$. In this ring, all the polynomials have degree at most $n-1$. For modular reduction $X^n$, it equals to $-1$ in this ring, namely $X \equiv -1$, while $X^{2n}$ equals to $1$.

And then further, we have the quotient ring $R_Q = R/Q$. The coefficients are computed modulo Q. For examples, $n=3$, $Q=5$:

\[\begin{array}{l} \left(x^{2}+x^{1}+2\right)\left(x^{2}-x^{1}-2\right)=x^{4}+0 x^{3}-1 x^{2}-4 x^{1}-4=-x^{2}+1 \\ \left(x^{2}+x^{1}+2\right)+\left(x^{2}-x^{1}-2\right)=2 x^{2} \end{array}\]

The most important parameters are $n$ and $\lceil\log Q\rceil$, which define the security. Almost all the efficient scheme based on the ring learning with error problem is a mathematical problem, and it is these two parameters we leverage to parameterize the security level. In general, for the purpose of efficient computing, $Q$ is usually a power of 2.

Encode & Encrypt

Message could be chosen from or integers modulo $t$ $\mathbb{Z}^n_t$ in BFV, where $t$ is the plaintext modulus, or complex integers $\mathbb{C}^{\frac{n}{2}}$ in CKKS.

The encoder maps a message vector to a plaintext polynomial in $R_t$ in BFV, and in $R$ in CKKS. Note that plaintexts are multiplied mod $t$ in BFV.

The encryptor maps a plaintext polynomial into a ciphertext in $R^2_Q$: ($ct_0$, $ct_1$), which is a pair of two polynomials. What is does is it actually adds noise to mask the secret, and then it randomizes the ciphertexts in each encryption(the same plaintexts give you different ciphertext each time).

Addition and multiplication are preserved in all three forms(message, plaintext & ciphertext)

Homomorphic Addition

Since we have two ciphertexts, we just simply add each polynomials together.

\[(c_0, c_1) = (a_0+b_0, a_1+b_1) \% q\]

In the case when $b$ is a plaintext, you just add $b$ to the first part

\[(c_0, c_1) =(a_0+b, a_1) \% q\]

The time complexity is $O(n)$ in terms of integer add mod $Q$. The noise’s variance grows $O(n^{0.5})$ in terms of number of homomorphic addition, and the noise budget is shrunken by 1 bit.

Homomorphic Multiplication

Homomorphic Multiplication actually give you three polynomials as results.

\[(c_0, c_1, c_2) = (a_0b_0,a_0,b_1+a_1b_0, a_1b_1) \% q\]

In the case when $b$ is a plaintext, you just multiply $b$ to both parts:

\[(c_0, c_1) = (a_0b, a_1b) \% q\]

And The decryption requires

\[[ct_0 + ct_1s + ct_2 s^2]_{q}\]

where $s$ is the private key.

The time complexity is $O(n log n)$ in terms of integer add/multiply mod Q under the acceleration technology NTT. Noise’s variance grows $O(c ^{\log n})$ in terms of numbers of homomorphic multiplication, and the noise budget is shrunken by many bits.

Relinearlization

Since we get more than two polynomials in the ciphertext after a homomorphic multiplication, if we want to do another multiplication, what do you do? There will be a lot more computation, and end up with more polynomials in a new ciphertext.

So there’s a step called relinearization follow. What is does is to convert these three polynomial ciphertexts to a new ciphertext with just two polynomials. It requires a linearization key, which is public key.

Rotation

So far, actually we have five functions: ciphertext addition, ciphertext and plaintext addition, ciphertext multiplication, ciphertext and plaintext multiplication & relinearization. This five functions should be enough to build, let say a polynomial evaluation or some basis algorithm.

We actually have one more. Since we are encoding a vector of numbers, you might want to rotate the hidden message slots of those numbers: (1,2,3,4, …) -> (3,4, …, 1,2)

There’s a faster way to do a rotation on an encrypted data, which requires something called the Galois Key which is also public key.

The time complexity is $O(n \log n \log Q)$ in terms of integer add/multiply mod Q. Additive noise may be introduced by negligible in Microsoft SEAL, and the noise budget is barely shrunken.

So here is combining operations:

Circuit Optimization

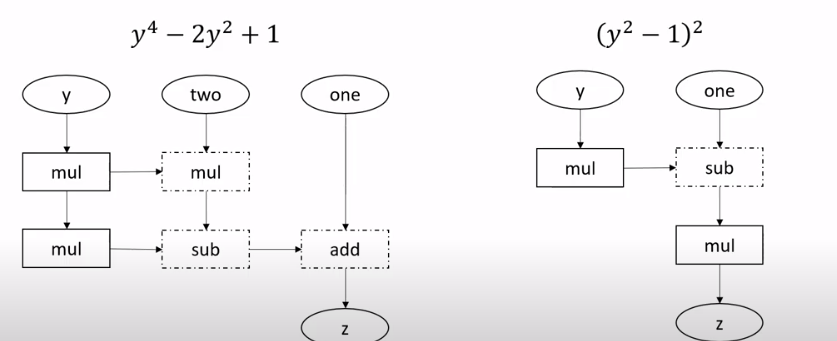
Notice that ciphertext-plaintext addition & multiplication introduce less noise. And generally, the length of critical path in above computation graph determines the noise.

Defining Computation

What kind of computation we can support? Actually, we can support linear functions: scalar, vector, and matrix/addition & multiplication. For examples, for polynomial evaluation with parallelism, a $k$ degree polynomial requires $\lceil \log k \rceil$ depth.

Equality check could be be quiet tricky. It has various algorithms in BFV, but not possible in CKKS.

Comparison is non-trivial, but no undoable. You can approximate the result with some high degree polynomials.

That technique applies to a non-linear function too, like sigmod. You can always approximate these nonlinear functions with a polynomial.

Decrypt & Decode

Decryption and Decode are just the reverse process of Encryption & encode.

$R_Q^2 \rightarrow R_t\ or\ R \rightarrow \mathbb{Z}_t^n\ or\ \mathbb{C}^{\frac{n}{2}}$

How does Encryption and Decryption work?

Basically, you generate a secret key $s$ as a polynomial from the ring. Usually a secret key can by just a ternary polynomial, which means the coefficients are $0$, $1$, or $-1$.

For example, we can support symmetric encryption of zero. You just generate an error $e$ , which is also polynomial from a discrete Gaussian distribution and gives you a random looking ciphertext. You also sample $a$, which is a polynomial uniformly sampled from $R_Q$.

\[\begin{align} e &\leftarrow \sigma \\ a &\leftarrow R_Q \\ ct &\leftarrow (-as+e, a) \in R_Q^2 \end{align}\]

$ct$ is a symmetric encryption cyphertext of an encryption of zero.

Also, we can use this as the public key $pk \leftarrow (-as+e, a) \in R_Q^2$. For example, if you want to do an asymmetric encryption of zero, you sample a ternary polynomial $u$ as private key $s$ above. And you generate two errors $e_0$ & $e_1$ as $e$ above.

\[\begin{align} e_0,e_1 &\leftarrow \sigma \\ u &\leftarrow ternary\ polynomial \\ ct &\leftarrow (pk_0u+e_0, pk_1u+e_1) \in R_Q^2 \end{align}\]

To encrypt a plaintext $m$, add plaintext to $ct_0$ with some modification:

\[\begin{align} e_0,e_1 &\leftarrow \sigma \\ u &\leftarrow ternary\ polynomial \\ ct &\leftarrow (pk_0u+e_0+\frac{Qm}{t}, pk_1u+e_1) \in R_Q^2 \end{align}\]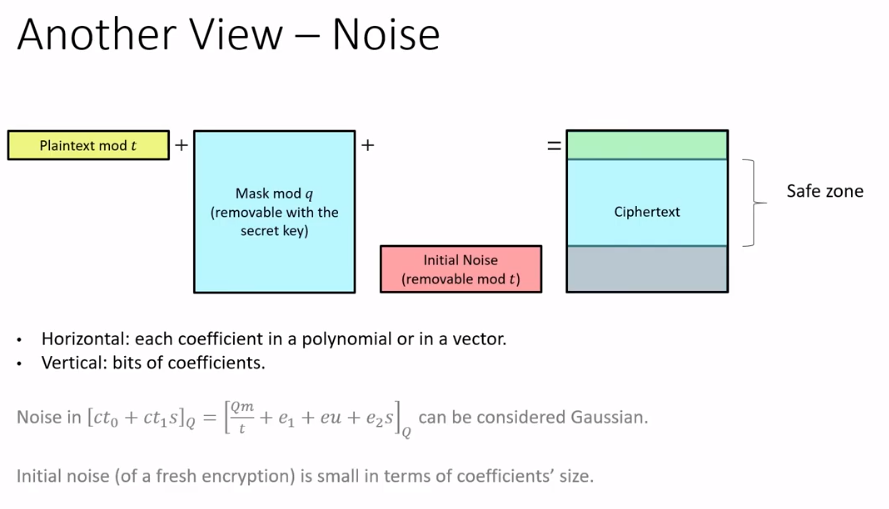

Decryption:

\[\left[c t_{0}+c t_{1} s\right]_{Q}=\left[\frac{Q m}{t}+e_{1}+e u+e_{2} s\right]_{Q}\]

Noise in decryption can be considered Gaussian.

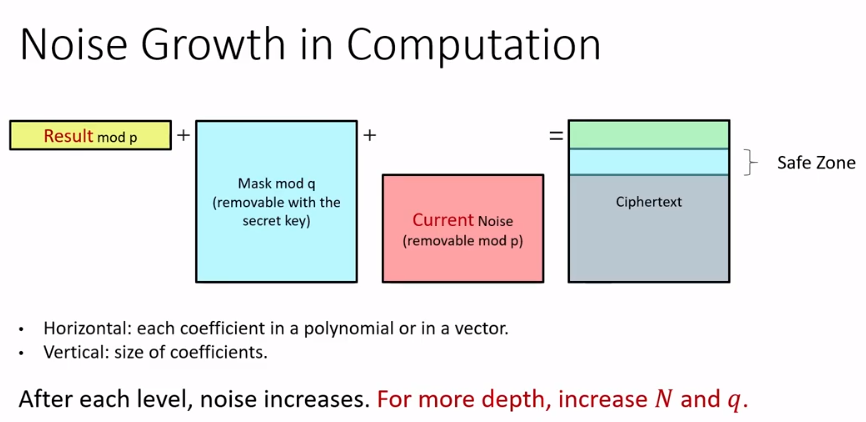
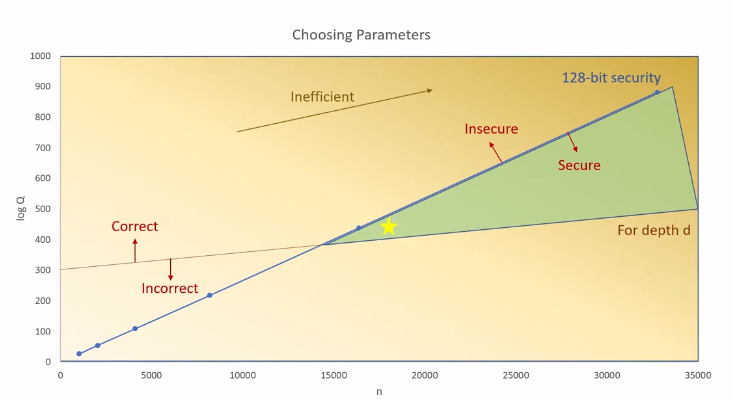
How to Setup Security Parameters?

Usually we require some attempts to find the proper $Q$. The best way is just start with a $Q$, try to evaluate the circuit, if it fails, increase the Q.

Notice that the larger the $Q$ is, the less secure the scheme is. So after you have decide the Q, you need to increase $n$.

Also, you can always choose parameters according to homomorphic encryption security standard at www.homomorphicencryption.org.

Full-RNS Variants

RNS refers to Residue Number System, which is similar to Chinese Remainder Theorem(CRT). Basically, you can represent a large integer with a set of smaller integers.

Modulus Switching

And there is another technology called Modulus Switching that makes computation more efficient. During the computation, you can discard a prime from that $Q$, so your ciphertext got smaller in terms of coefficients.

How to Setup Performance Parameters?

In the example, You can use RNS by either write in four prime numbers as a vector, or just tell the SEAL to create four prime numbers having 40 bits, 40 bits, 40 bits and 50 bits, under which condition the Q size cannot be more than 170 bits.

How to design A circuit?

Misc