从Partial CUDA Graph到Full CUDA Graph
在上一篇深入理解 Megatron-LM 中的 Partial CUDA Graph:MoE 模型训练加速的关键技术中,我们分析了在MoE训练流程中,影响CUDA Graph兼容性的主要瓶颈是MoE部分的动态行为。在本文中,我们将深入探讨,为了使MoE部分能够无缝地融入CUDA Graph,并最终实现包含前向与反向传播在内的完整iteration的Full CUDA Graph捕获,需要对其结构做出哪些关键性改进。
具体而言,MoE与CUDA Graph的兼容性亟需解决以下三项核心技术难题:
- 排除TE grouped GEMM中的CPU-GPU同步环节,实现与CUDA Graph的原生兼容;
- 对HybridEP策略进行重构,使其运行逻辑与CUDA Graph协同无障碍; 实际上,完成上述两项优化后,在MoE强制负载均衡(load balancing)的设定下,已能够实现真正意义上的Full CUDA Graph。然而,由于HybridEP与CUDA Graph兼容性提升带来的静态缓冲区约束,我们还需进一步实现高效的Expert权重分发及梯度聚合机制,以充分释放CUDA Graph的性能潜力。
如何让TE启动grouped GEMM不需要GPU-CPU同步?
在MoE中,由于每个experts分到的token数量不同,实际上我们是在做grouped GEMM,通常我们会调用transformer engine (TE)的grouped GEMM,也就是在调用TE的pytorch.GroupedLinear类。
一般来说,TE实现grouped GEMM主要是通过两个后端实现方式。
- 调用cuBLAS作为后端实现方式。但是当前cuBLAS实际上并没有真正实现单个kernel launch grouped GEMM的形式,实际上TE是循环调用多次cuBLAS kernel并分发到不同CUDA stream上实现的(见下图的左图)。
- 另外一个后端实现方式是cutlass。cutlass是有单个kernel launch grouped GEMM的支持的(见下图的右图)。
我们可以通过环境变量NVTE_USE_CUTLASS_GROUPED_GEMM来控制使用cuBLAS还是cutlass。但是目前至少在TE 2.12版本里面,这个环境变量只对H系列GPU起作用,在B系列上即使设置了这个环境变量也还是会fallback到使用cuBLAS中。在H系列芯片中,multi-stream的方式做grouped GEMM更快,但是在B系列芯片上,cuBLAS更快,因此我们后面的实现都考虑是cuBLAS作为后端。
TE 2.12启动grouped GEMM会有GPU-CPU同步主要是torch.split这个API带来的。在TE 2.12版本版本的代码中,有这么一项:
inputmats = torch.split(cast_if_needed(inp_view, activation_dtype), m_splits_list)
torch.split要求m_splits_list这一项必须在CPU上。torch.split(inp_view, m_splits_list) 会将输入 tensor inp_view 按照 m_splits_list 中指定的大小切分成多个子 tensor,每个子 tensor 对应一个 expert 的输入。
m_splits_list就是tokens_per_expert,因此在Megatron-LM中,需要将tokens_per_expert从GPU转到CPU list。tokens_per_expert需要通过 .cpu().tolist() 将GPU上的tensor转换为CPU上的Python list。这个操作会触发GPU-CPU同步。
从另外一个层面上看,在TE 2.12版本中,m_splits虽然作为了参数传到到C++层面的te_general_grouped_gemm,但是其实并没有用到,因为信息已经通过torch.split编码在 A[i].shape[0] 中。
但是在CUDA Graph的要求下,我们不能有GPU-CPU同步。因此我们需要把m_splits 作为 GPU tensor 传给 kernel,通过GPU操作完成类似torch.split的功能。
具体实现可以参考这个文件,此文件完成了TE 2.12还没有做到事情,·1)实现了在B系列上支持cuBLAS作为后端,2)不需要CPU-GPU同步来完成类似torch.split的功能。
对于第2点,其核心思想是,在启动 CUTLASS Grouped GEMM前,用一个轻量级 GPU kernel (setGroupedGemmArguments_fp16bf16) 来读取 GPU 上的 m_splits 并配置 GEMM 参数,整个过程无需 CPU 参与,因此不会触发 CPU-GPU 同步,使得 MoE 层可以完全被 CUDA Graph 捕获。
__global__ void setGroupedGemmArguments_fp16bf16(int num_experts, const int64_t *gemm_m_per_expert,
int gemm_n, int gemm_k, ElementA *ptr_A, ElementD *ptr_D,
UnderlyingProblemShape *problem_sizes,
ElementA **ptr_A_list, StrideA *stride_A_list, StrideB *stride_B_list,
ElementD **ptr_D_list, StrideD *stride_D_list) {
uint64_t m_offset = 0;
if (threadIdx.x == 0 && blockIdx.x == 0) { // 只用一个线程执行
for (int expert_id = 0; expert_id < num_experts; expert_id++) {
int gemm_m = int(gemm_m_per_expert[expert_id]); // <-- 直接从GPU读取m_splits
problem_sizes[expert_id] = cute::make_shape(gemm_m, gemm_n, gemm_k);
ptr_A_list[expert_id] = ptr_A + m_offset * gemm_k; // 计算每个expert的A指针
stride_A_list[expert_id] = cute::make_stride(int64_t(gemm_k), _1{}, _0{});
// ...
ptr_D_list[expert_id] = ptr_D + m_offset * gemm_n; // 计算每个expert的D指针
stride_D_list[expert_id] = cute::make_stride(int64_t(gemm_n), _1{}, _0{});
m_offset += gemm_m; // 累加偏移
}
}
}
对于第一点(实现了在B系列上支持cuBLAS作为后端),相关函数的函数名为generic_moe_gemm_kernelLauncher_fp16bf16,主要分为 4 个主要阶段:
- 阶段 1:定义CUTLASS 类型。使用 CUTLASS 的 Builder 模式定义高性能 Grouped GEMM kernel 的所有类型参数。
// 定义 GEMM 问题形状
using ProblemShape = cutlass::gemm::GroupProblemShape<Shape<int, int, int>>; // <M,N,K>
// 配置矩阵类型和布局
using ElementA = ElementInput; // FP16 或 BF16
using LayoutA = cutlass::layout::RowMajor;
using ElementAccumulator = float; // 累加器用 FP32
// 核心配置:针对 SM100 (Blackwell) 架构
using ArchTag = cutlass::arch::Sm100;
using MmaTileShape = Shape<_256, _256, Int<128 / sizeof(ElementA)>>; // Tile 大小
using KernelSchedule = cutlass::gemm::KernelPtrArrayTmaWarpSpecialized2SmSm100; // TMA调度
// 构建 GEMM kernel
using GemmGrouped = cutlass::gemm::device::GemmUniversalAdapter<GemmKernel2SM>;
- 阶段 2:Workspace 内存布局。在预分配的 GPU workspace 中划分内存区域,用于存储各 expert 的参数。
// 在 workspace 中分配各种指针数组和 stride 数组
auto ptr_A_list = ...; // 每个 expert 的 A 矩阵指针
auto ptr_D_list = ...; // 每个 expert 的 D(输出)矩阵指针
auto stride_A_list = ...; // 每个 expert 的 A stride
auto stride_B_list = ...; // 每个 expert 的 B stride
auto stride_D_list = ...; // 每个 expert 的 D stride
auto problem_sizes = ...; // 每个 expert 的 GEMM shape (M, N, K)
- 阶段 3:启动参数设置 Kernel。启动一个小型 GPU kernel,在 GPU 上读取 gemm_m_per_expert(m_splits),并填充:
- problem_sizes[i] = (M_i, N, K) —— 每个 expert 的 GEMM 形状
- ptr_A_list[i] —— 每个 expert 的输入指针
- ptr_D_list[i] —— 每个 expert 的输出指针
- 各种 stride
setGroupedGemmArguments_fp16bf16<<<1, 32, 0, stream>>>(
num_experts, gemm_m_per_expert, // <-- m_splits (GPU tensor)
gemm_n, gemm_k, ptr_A, ptr_D, problem_sizes,
ptr_A_list, stride_A_list, stride_B_list,
ptr_D_list, stride_D_list);
- 阶段 4:启动 CUTLASS Grouped GEMM。使用阶段 3 在 GPU 上设置好的参数,启动 CUTLASS Grouped GEMM kernel。
// 构建 CUTLASS 参数
args = typename GemmGrouped::Arguments{
cutlass::gemm::GemmUniversalMode::kGrouped,
{num_experts, problem_sizes, nullptr}, // 问题形状(在 GPU 上)
{ptr_A_list, stride_A_list, ptr_B_list, stride_B_list}, // 输入
{fusion_args, nullptr, stride_D_list, ptr_D_list, stride_D_list}, // 输出
hw_info, scheduler
};
// 初始化并运行
gemm.initialize(args, workspace + offset);
gemm.run(stream); // 执行 Grouped GEMM
HybridEP支持CUDA Graph后有什么限制?
Megatron的Full CUDA Graph支持
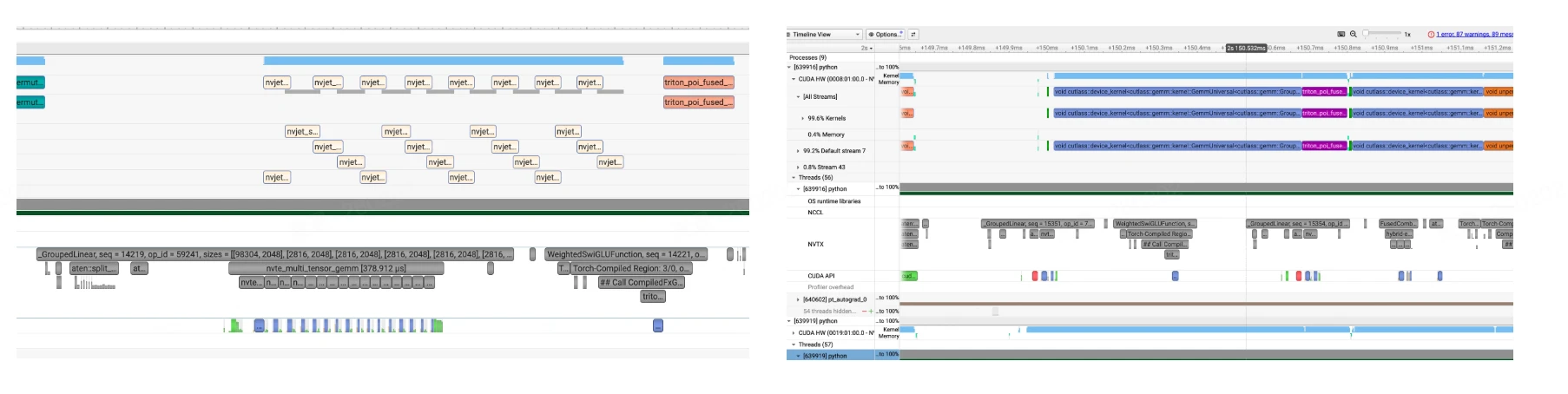
另外一个问题时,Megatron的Full CUDA Graph是否支持PP?,实际上Full CUDA Graph捕获的是整个 forward_backward_func 的执行,而不是单个 layer 或单个 stage。forward_backward_func 内部会处理所有 PP stages 的前向传播、反向传播以及 microbatch 的调度(如 1F1B 调度)。因此一个 CUDA Graph 就包含了所有 PP stages 的计算,所有 microbatches 的处理以及PP stages 之间的通信(send/recv)。
if curr_iteration == self.cuda_graph_warmup_steps:
logger.info(f'Capture CUDA graph for {training_str}!!!')
torch.distributed.barrier()
assert FullCudaGraphWrapper.cuda_graph[training_str] is None
FullCudaGraphWrapper.cuda_graph[training_str] = torch.cuda.CUDAGraph()
# ... 注册 RNG states
with torch.cuda.graph(
FullCudaGraphWrapper.cuda_graph[training_str],
stream=capture_stream,
capture_error_mode="thread_local",
):
# 捕获整个 forward_backward_func,包含所有 PP stages
FullCudaGraphWrapper.result[training_str] = self.forward_backward_func(
*args, **kwargs
)
同时我们也能看到,在数据读取上是支持多stage PP的:
def data_read(self, data_iterator, model, training, num_microbatches):
"""Read all microbatch inputs from Dataloader and copy to static buffers."""
if not isinstance(model, list) or len(model) == 1:
# 单 stage 场景(无 PP 或 PP size = 1)
assert not isinstance(data_iterator, list) or len(data_iterator) == 1
# ... 处理单个 data_iterator
else:
# 多 stage 场景(PP size > 1)
assert isinstance(data_iterator, list) and len(data_iterator) == len(model)
data_list = []
for i in range(len(model)):
if data_iterator[i] is not None:
# 为每个 PP stage 分别读取 microbatch 数据
data_list_i = []
for b in range(num_microbatches):
data_list_i.append(...)
data_list.append(iter(data_list_i))
else:
data_list.append(None)
因此无论 PP 有多少个 stage,只会创建 2 个 CUDA Graph:1 个用于 training,1 个用于 validation。
curr_iteration = {'training': 0, 'validation': 0}
cuda_graph = {'training': None, 'validation': None}
result = {'training': None, 'validation': None}
Expert权重分发与梯度收集机制
sequenceDiagram
participant Input as Hidden States
participant Router
participant Planner as Offloading Planner
participant ExpertDisp as Expert Dispatcher
participant TokenDisp as Token Dispatcher
participant Experts
participant Output
Input->>Router: hidden_states
Router->>Planner: routing_map, probs
Planner->>Planner: gen_offloading_plan()
Planner->>ExpertDisp: expert_offloading_map
ExpertDisp->>Experts: dispatch weights to echo experts
Input->>TokenDisp: hidden_states, rerouted_probs
TokenDisp->>Experts: dispatched tokens
Experts->>TokenDisp: expert outputs
TokenDisp->>Output: combined output
如何决定home experts复制到哪些redundant expert slots?
gen_intermediate是为了计算每个EP rank的空闲容量和每个local expert的计算溢出量:
def gen_intermediate(count_tokens_per_expert_from_ep_rank, ...):
# 步骤1: 计算每个EP rank的token总数和平均值
count_tokens_per_ep_rank = count_tokens_per_expert.view(num_ep_ranks, -1).sum(dim=1)
avg_tokens_per_ep_rank = count_tokens_per_ep_rank.sum() // num_ep_ranks
# 步骤2: 计算spare容量 = max(0, avg - current)
# 负载低于平均的EP rank有空闲容量接收tokens
deviation = count_tokens_per_ep_rank - avg_tokens_per_ep_rank
capacity_spare_per_ep_rank = torch.relu(-deviation)
# 步骤3: 计算spillover(溢出量)
# 关键思路:对每个EP rank内的专家按token数排序,
# 累积求和后超过平均值的部分就是spillover
count_tokens_sorted, indices_sorted = count_tokens_per_expert.view(num_ep_ranks, -1).sort(dim=1)
spillover_cumsum = (count_tokens_sorted.cumsum(dim=1) - avg_tokens_per_ep_rank).clamp(min=0)
# 从cumsum转回每个专家的spillover
count_spillover_sorted = torch.cat([spillover_cumsum[:, :1],
torch.diff(spillover_cumsum, dim=1)], dim=1)
capacity_spare_per_ep_rank是一个EP Rank层级的变量,表示当前EP Rank超出了多少token需要重新分配,这个很好理解:
avg = 350
│
EP0: 500 ■■■■■■■■■■■■■■■│■■■■ 超额 150 → spillover
EP1: 200 ■■■■■■ │ 空闲 150 → spare capacity
EP2: 300 ■■■■■■■■■ │ 空闲 50 → spare capacity
EP3: 400 ■■■■■■■■■■■■ │■ 超额 50 → spillover
│
okk。现在我们知道了本地EP rank应该要offload多少token出来,但是一个EP rank有多个local expert,我们怎么知道每个expert应该要分多少token出来。使得这个数刚好等于本地的capacity_spare_per_ep_rank?
计算spillover的直观理解:假设一个 EP rank 有 4 个专家,tokens 分布为 [50, 100, 150, 200],平均值为 250(注意这个平均值是所有EP rank的平均值):
- 排序后: [50, 100, 150, 200]
- 累积和: [50, 150, 300, 500]
- 减去平均值后: [-200, -100, 50, 250]
- clamp(min=0): [0, 0, 50, 250]
- 差分得到spillover: [0, 0, 50, 200]。 我们看到,token数总和为1000,
一个要思考的问题为什么我们这里要先做累积和然后做差分得到spillover?直接tokens 分布减去平均值可以吗? 我们先考虑直接减法有什么问题:
spillover = (tokens_per_expert - avg_per_expert).clamp(min=0)
# avg_per_expert = 250 / 4 = 62.5
# 结果:
专家0: (50 - 62.5).clamp(0) = 0
专家1: (100 - 62.5).clamp(0) = 37.5
专家2: (150 - 62.5).clamp(0) = 87.5
专家3: (200 - 62.5).clamp(0) = 137.5
───────────────────────────────────
总 spillover: 262.5 tokens ← 超过了需要的 250!
这样的问题是这样计算会导致 spillover 过多,因为每个专家独立判断”超额”。
如果我们采用前缀和加上差分的思想:
# Step 1: 排序(从小到大)
sorted_tokens = [50, 100, 150, 200]
# Step 2: 累积和
cumsum = [50, 150, 300, 500]
# Step 3: 减去平均值并 clamp
spillover_cumsum = ([50, 150, 300, 500] - 250).clamp(min=0)
= [-200, -100, 50, 250].clamp(min=0)
= [0, 0, 50, 250]
# Step 4: 差分得到每个专家的 spillover
spillover = [0, 0-0, 50-0, 250-50]
= [0, 0, 50, 200]
总 spillover: 250 tokens ← 正好等于超额部分!
其核心思想是当累积和超过平均值时,才开始 spillover;同时差分将”整体超额”按贡献分配给各专家。
tokens: 50 100 150 200
│ │ │ │
cumsum: 50 ──── 150 ──── 300 ──── 500
│ │ │ │
│ │ │ │
avg=250 ────│────────│────────┼────────│────
│ │ ↑ ↑
│ │ 超出50 超出250
│ │ │ │
spillover: 0 0 50 200
└────────┘
差分: 250-50=200
另外,我们排序为了让负载轻的专家优先保留自己的 tokens:
未排序 [200, 50, 150, 100]:
cumsum = [200, 250, 400, 500]
spillover_cumsum = [0, 0, 150, 250] ← 从专家0开始就接近平均值
spillover = [0, 0, 150, 100]
排序后 [50, 100, 150, 200]:
cumsum = [50, 150, 300, 500]
spillover_cumsum = [0, 0, 50, 250] ← 更晚才超过平均值
spillover = [0, 0, 50, 200]
排序后,小专家贡献的 spillover 更少,大专家贡献更多,这样可以更公平的负载均衡。
有了这个数值之后,我们使用贪心分配算法one_shot_greedy_assignment:来求解这个问题:
def one_shot_greedy_assignment(count_tokens_per_chunk, capacity_per_bucket):
"""
使用区间重叠计算实现一次性贪心分配
原理:
- 将所有token chunks看作连续区间 [start, end)
- 将所有bucket容量看作连续区间 [start, end)
- 计算每对 (chunk, bucket) 的区间重叠作为分配量
"""
# 计算累积和得到区间端点
chunks_cumsum = torch.cumsum(count_tokens_per_chunk, dim=0)
buckets_cumsum = torch.cumsum(capacity_per_bucket, dim=0)
chunk_start = chunks_cumsum - count_tokens_per_chunk # [0, c1, c1+c2, ...]
chunk_end = chunks_cumsum # [c1, c1+c2, ...]
bucket_start = buckets_cumsum - capacity_per_bucket
bucket_end = buckets_cumsum
# 计算重叠
overlap_start = torch.maximum(chunk_start[:, None], bucket_start[None, :])
overlap_end = torch.minimum(chunk_end[:, None], bucket_end[None, :])
assignment = (overlap_end - overlap_start).clamp(min=0)
举个例子:chunks = [100, 150], buckets = [80, 120]
chunks: |---100---|---150---|
buckets: |--80--|----120----|
cumsum: [100, 250] 和 [80, 200]
chunk区间: [0,100), [100,250)
bucket区间: [0,80), [80,200)
重叠矩阵:
bucket0 bucket1
chunk0 [0,80)∩[0,100)=80 [80,100)∩[100,250)=0 → [80, 0]
chunk1 [0,80)∩[100,250)=0 [80,200)∩[100,250)=100 → [0, 100]
# 每个专家的 spillover(已计算好)
count_spillover_per_home_expert = [0, 80, 0, 0, 50, 100, 0, 30]
# 专家编号: 0 1 2 3 4 5 6 7
# 每个 EP rank 的 spare capacity
capacity_spare_per_ep_rank = [0, 120, 60, 0]
# EP rank: 0 1 2 3
# 对 spillover 降序排序
count_spillover_sorted = [100, 80, 50, 30, 0, 0, 0, 0]
indices_spillover_sort = [5, 1, 4, 7, 0, 2, 3, 6] # 原始专家编号
# 对 spare capacity 降序排序
capacity_spare_sorted = [120, 60, 0, 0]
indices_spare_sort = [1, 2, 0, 3] # 原始 EP rank 编号
为什么排序? 把最大的 spillover 和最大的 capacity 排在前面,方便贪心分配。
这是核心算法,使用区间重叠技术:
def one_shot_greedy_assignment(chunks, buckets):
"""
chunks = spillover_sorted = [100, 80, 50, 30, 0, 0, 0, 0] (待分配的量)
buckets = capacity_sorted = [120, 60, 0, 0] (可接收的容量)
"""
chunks 累积和: [100, 180, 230, 260, 260, 260, 260, 260]
buckets 累积和: [120, 180, 180, 180]
chunks 区间:
chunk 0: [0, 100) spillover=100
chunk 1: [100, 180) spillover=80
chunk 2: [180, 230) spillover=50
chunk 3: [230, 260) spillover=30
chunk 4-7: 空 (spillover=0)
buckets 区间:
bucket 0: [0, 120) capacity=120
bucket 1: [120, 180) capacity=60
bucket 2-3: 空 (capacity=0)
0 100 120 180 230 260
│ │ │ │ │ │
chunks: │◄─chunk0─┼─────────►◄chunk1─►│◄chunk2─►│◄chunk3►│
│ 100 │ │ 80 │ 50 │ 30 │
│ │ │ │ │ │
buckets: │◄──────bucket0────►│◄bucket1►│ │ │
│ 120 │ 60 │ │ │
│ │ │ │ │ │
重叠矩阵 [8 experts × 4 ep_ranks]:
bucket0 bucket1 bucket2 bucket3
[0,120) [120,180) [180,180) [180,180)
chunk0 [0,100) 100 0 0 0
chunk1 [100,180) 20 60 0 0
chunk2 [180,230) 0 0 0 0 (bucket1 结束于 180)
chunk3 [230,260) 0 0 0 0
chunk4-7 0 0 0 0
assignment_sorted =
[[100, 0, 0, 0],
[ 20, 60, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0]]
当 num_spare_experts_per_ep_rank > 1 时,每个 EP rank 可以接收多个专家的 offload:
假设 num_spare_experts_per_ep_rank = 2:
EP1 有 2 个 spare experts,可以接收 2 个不同专家的 offload
→ 从 assignment 矩阵的 EP1 列中选 top-2 个最大值
→ 得到 2 个 (home_expert, offload_amount) 对
gen_assignment / one_shot_greedy_assignment 只决定了:
- 专家级别的分配:”专家 A 要 offload 100 tokens 到 spare expert X” 但它没有决定:
- EP rank 级别的分配:”专家 A 的 100 tokens 中,多少来自 EP0,多少来自 EP1…” 因为同一个专家可能收到来自多个 EP ranks 的 tokens!
专家 A (home expert)
总 spillover = 100
│
┌─────────────────┼─────────────────┐
│ │ │
来自 EP0 来自 EP1 来自 EP2
30 tokens 50 tokens 20 tokens
│ │ │
└─────────────────┼─────────────────┘
│
▼
需要决定怎么分配!
两阶段分配流程
┌─────────────────────────────────────────────────────────────────────────────┐
│ 两阶段分配流程 │
├─────────────────────────────────────────────────────────────────────────────┤
│ │
│ 输入: count_tokens_per_expert_from_ep_rank [ep_size, num_experts] │
│ count_tokens_from_home_expert_to_spare_expert [num_experts, num_spare]│
│ │
│ ┌─────────────────────────────────────────────────────────────────┐ │
│ │ Phase 1: breadth_first_allocation (广度优先) │ │
│ │ │ │
│ │ 策略:按比例分配,让每个 EP rank 公平贡献 │ │
│ │ │ │
│ │ EP0 贡献: 30/100 * capacity = 30% 的 offload 量 │ │
│ │ EP1 贡献: 50/100 * capacity = 50% 的 offload 量 │ │
│ │ EP2 贡献: 20/100 * capacity = 20% 的 offload 量 │ │
│ │ │ │
│ │ 使用 floor() 取整,可能有剩余 │ │
│ └─────────────────────────────────────────────────────────────────┘ │
│ │ │
│ ▼ │
│ ┌─────────────────────────────────────────────────────────────────┐ │
│ │ Phase 2: depth_first_allocation (深度优先) │ │
│ │ │ │
│ │ 处理 Phase 1 的取整误差导致的剩余容量 │ │
│ │ 使用区间重叠算法填满剩余空间 │ │
│ └─────────────────────────────────────────────────────────────────┘ │
│ │ │
│ ▼ │
│ 输出: 每个 EP rank 具体 offload 多少 tokens 到每个 spare expert │
│ │
└─────────────────────────────────────────────────────────────────────────────┘
3 个 EP ranks,专家 A 的 tokens 分布:
- 来自 EP0: 30 tokens
- 来自 EP1: 50 tokens
- 来自 EP2: 20 tokens
- 总计: 100 tokens
gen_assignment 决定: 专家 A offload 80 tokens 到 spare expert X
Phase 1: breadth_first_allocation(按比例分配)
# 找到主要供应者(argmax)
idx_supplier = argmax([专家A的offload量]) = 专家A
# 计算每个 EP rank 的贡献比例
count_tokens_rel = [30, 50, 20] # 各 EP rank 发给专家 A 的 tokens
probs_proportional = [30/100, 50/100, 20/100] = [0.3, 0.5, 0.2]
# 按比例分配 capacity=80
count_tokens_ideal = [0.3*80, 0.5*80, 0.2*80] = [24, 40, 16]
# 取整(floor)
count_tokens_floors = [24, 40, 16] # 正好,无余数
结果是:
EP0 offload 24 tokens 到 spare X
EP1 offload 40 tokens 到 spare X
EP2 offload 16 tokens 到 spare X
─────────────────────────────────
总计: 80 tokens ✓
如果有取整误差?怎么办?
假设 capacity = 83(不能被整除)
count_tokens_ideal = [0.3*83, 0.5*83, 0.2*83] = [24.9, 41.5, 16.6]
count_tokens_floors = floor([24.9, 41.5, 16.6]) = [24, 41, 16]
总计 = 24 + 41 + 16 = 81 < 83
剩余容量 = 83 - 81 = 2 tokens
Phase 2: depth_first_allocation(填充剩余)
# 剩余容量
capacity_spare_remaining = 2
# 各 EP rank 剩余可 offload 的 tokens
# EP0: 30 - 24 = 6 tokens 还没 offload
# EP1: 50 - 41 = 9 tokens 还没 offload
# EP2: 20 - 16 = 4 tokens 还没 offload
# 使用区间重叠贪心分配
# 按 EP rank 顺序(EP0 → EP1 → EP2)填充剩余容量 2
# EP0 再贡献 2 tokens(因为 6 > 2)
second_pass_offload = [2, 0, 0]
最终结果是:
EP0 offload: 24 + 2 = 26 tokens
EP1 offload: 41 + 0 = 41 tokens
EP2 offload: 16 + 0 = 16 tokens
─────────────────────────────────
总计: 83 tokens ✓
为什么叫为什么叫”广度优先”和”深度优先”?
专家A 专家B 专家C
│ │ │
┌──────────┼──────────┐ │ ┌──────────┼──────────┐
│ │ │ │ │ │ │
EP0 EP1 EP2 ... ...
广度优先 (Breadth-First):
先按比例分配所有专家的所有 EP ranks
→ 横向扫描,保证公平性
深度优先 (Depth-First):
处理剩余,一个专家一个专家地填满
→ 纵向扫描,最大化利用率
两阶段设计保证了:
- 公平性:各 EP rank 按比例贡献(广度优先)
- 完整性:剩余容量被完全利用(深度优先)
每个EP rank都运行gen_offloading_plan算法,得到的结果是一样的吗?
每个 EP rank 都独立运行这个算法。关键在于输入的构成:
# Step 1: 局部信息 - 每个 EP rank 不同
tokens_per_expert_local = routing_map.sum(dim=0).long() # 本 EP rank 的 token 分布
# Step 2: 全局信息 - 通过 AllGather 收集,所有 EP ranks 相同
tokens_per_expert_per_ep_rank = gather_from_sequence_parallel_region(
tokens_per_expert_local,
group=self.ep_group,
).reshape(ep_size, num_experts) # [ep_size, num_experts]
# Step 3: 调用 gen_offloading_plan
rerouted_routing_map, rerouted_probs, expert_offloading_map = gen_offloading_plan(
map_token_to_expert=routing_map, # 局部:每个 EP rank 不同
probs_routing=probs, # 局部:每个 EP rank 不同
count_tokens_per_expert_from_ep_rank=tokens_per_expert_per_ep_rank, # 全局:相同
ep_rank=ep_rank, # 不同:0, 1, 2, ...
num_ep_ranks=ep_size, # 相同
...
)
在gen_offloading_plan内部,expert_offloading_map 所有 EP ranks 相同,因为这个映射只依赖于 count_tokens_per_expert_from_ep_rank(全局 token 分布),与局部 routing_map 无关。
# gen_offloading_plan 内部
count_tokens_from_home_expert_to_spare_expert = gen_assignment(
count_tokens_per_expert_from_ep_rank, # 全局相同的输入
...
)
map_home_expert_to_spare = count_tokens_from_home_expert_to_spare_expert > 0
但是rerouted_routing_map 和 rerouted_probs每个 EP rank 不同,因为每个 EP rank 只重路由自己的 tokens。
# reroute_tokens_triton 使用局部信息
map_token_to_all_experts, probs_rerouted = reroute_tokens_triton(
map_token_to_expert, # 局部 routing_map
probs_routing, # 局部 probs
count_tokens_offloaded_from_ep_rank[ep_rank], # 根据 ep_rank 选择
count_tokens_offloaded_to_spare[ep_rank], # 根据 ep_rank 选择
...
)