写在前面
RePlAce 是 2019 年发表在 TCAD 的一篇论文,这篇论文作者之一是 VLSI CAD 界内著名的Andrew B. Kahng教授,并且现在已经集成到开源芯片设计工具 OpenROAD 中。
标题:RePlAce: Advancing Solution Quality and Routability Validation in Global Placement
作者:Chung-Kuan Cheng, Andrew B. Kahng, Ilgweon Kang, and Lutong Wang
机构:UCSD
发表会议:TCAD 2019
链接:https://ieeexplore.ieee.org/document/8418790
代码:https://github.com/The-OpenROAD-Project/RePlAce
方法简介
RePlAce 是一个支持混合尺寸(即 mixed-size,布局对象包括 standard cells 和 macros)和可路由性驱动(routability-driven)的全局布局框架。RePlAce 在 基于静电场系列(ePlace series)的布局算法上发展过来,使用了全局布局(Global Router)器 NCTU-GR 来估计路由拥塞情况,并使用 NTUPlace3 作为详细布局器。RePlAce 主要的改进之处有三点:
-
引入局部密度(local density)项来减少局部拥塞。
-
改进之前的动态自适应步长(Improved Dynamic Step Size Adaptation)。
-
基于全局布局器 NCTU-GR 和面积放大(cell inflation)策略的金属层感知(layer-aware)可路由性驱动布局算法。
实验结果表明,在 ISPD 2005 和 ISPD 2006 数据集上优化了 2.00%的半周长线长(half-perimeter wirelength,HPWL),在 MMS 数据集上优化了 2.73%的 HPWL,并在 DAC 2012 Routability-driven Placement 和 ICCAD 2012 global routability-driven placement 数据集上优化了 8.50-9.59%的 scaled HPWL。
我们首先来看 RePlAce 的整体布局框架:
整体布局框架
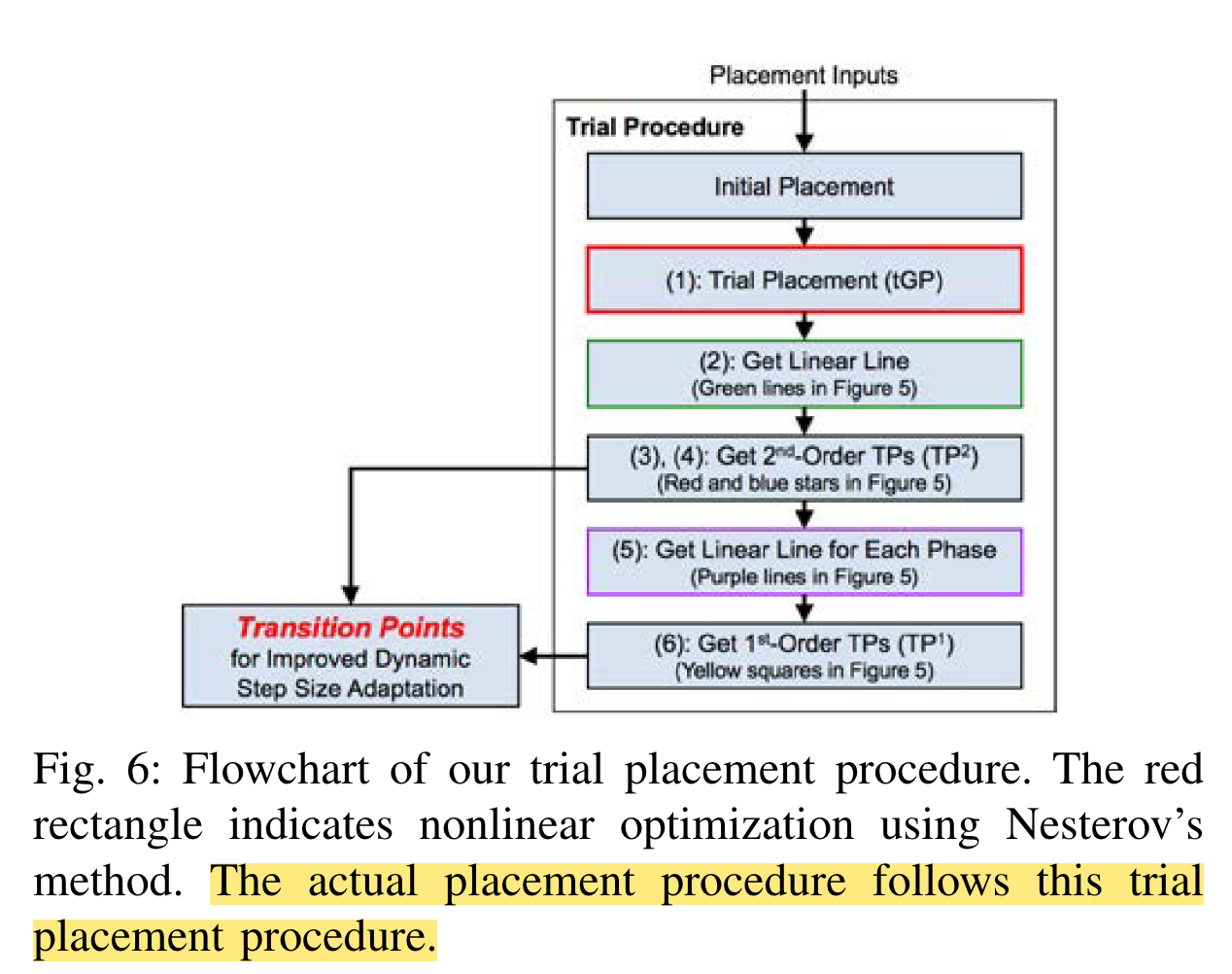
整体的布局框架分为两部分,第一部分是为了获取动态自适应步长的试验性布局(trial placement),第二部分是在第一部分得到的自适应步长上再次进行布局(actual placement),最后输出结果。
 |
 |
|---|---|
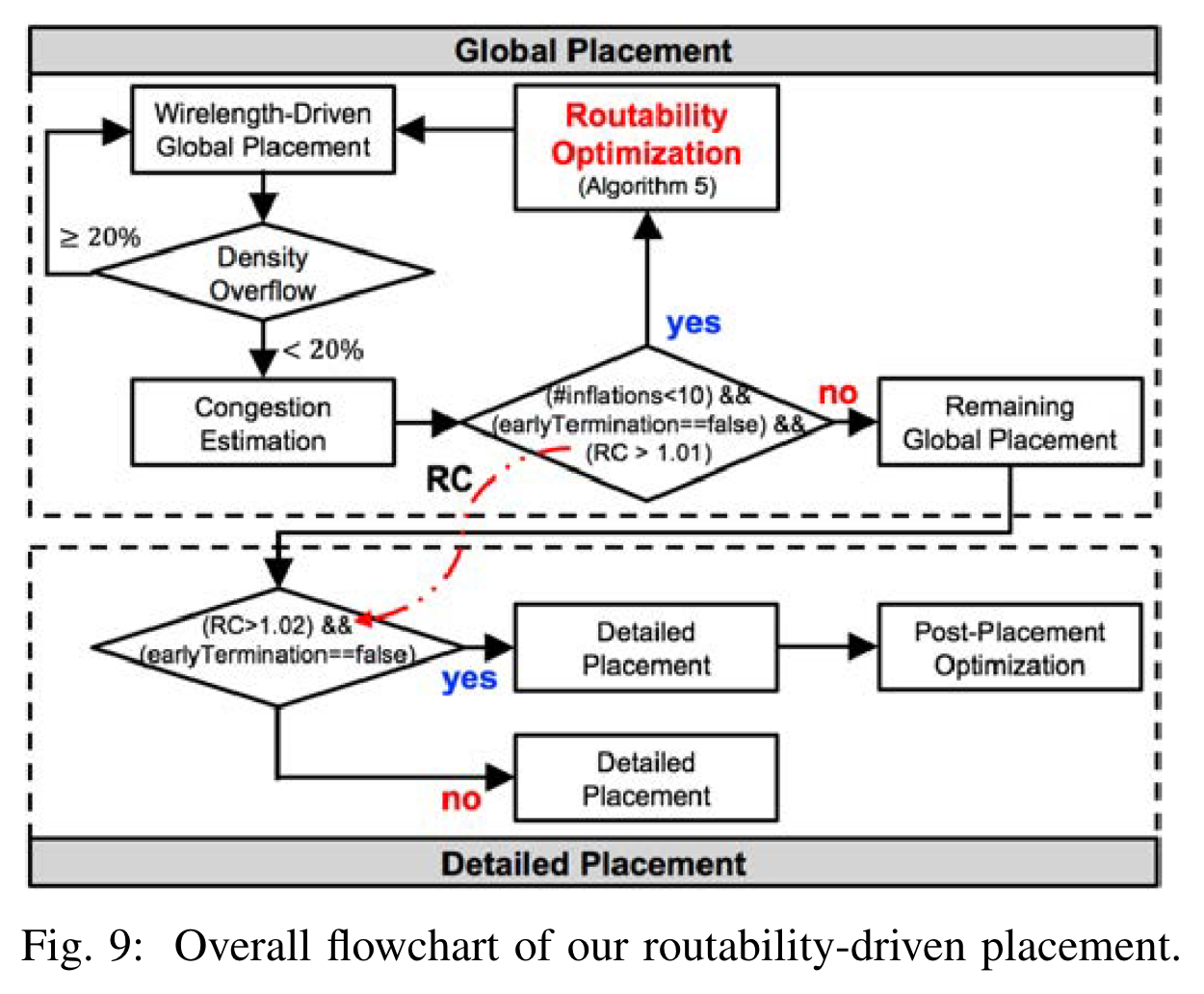
| trial Global Placement (tGP) | Acutal Placement |
先看右侧的 actual placement, 首先 RePlAce 进行线长驱动的全局布局,当 density overflow 下降到 20%时,使用全局布局器 NCTU-GR 估计路由拥塞,并根据如图的三个条件判断是否需要进行基于面积放大策略的可路由性优化。其中这里的三个条件中两个需要解释一下:
-
一个是路由拥塞(Routing Congestion, RC)值。这个是使用 DAC 2012 benchmark 官方提供的脚本测量的。RC>1.01 意味着有超过 1%的 routing overflow。RC 数值越大,说明路由拥塞越严重。
-
另外一个是作者设置的标志 earlyTermination。RePlAce 认为当earlyTermination为真时,可路由性优化算法已经没有优化空间了,就直接退出。当在过去连续四次可路由性优化中,最小的 RC 值没有减少 0.008 时,earlyTermination就会设为真。
在全局布局之后,RePlAce 使用了 NTUPlace3 作为详细布局器。并且当 RC>1.02 且earlyTermination为假时,RePlAce 认为还有进一步的优化空间,并使用1进一步优化布局结果。
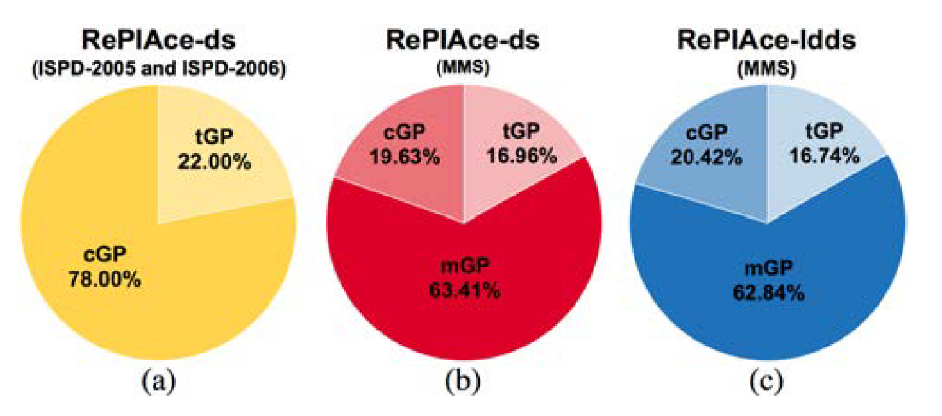
此外,对于 macros,RePlAce 先经历了混合大小全局布局(mGP)阶段,接着使用模拟退火算法合法化 macro 位置,接着进入只有标准单元的全局布局阶段(cGP)。
我们接下来分别看 RePlAce 三个主要改进的地方:
引入局部密度项来减少局部拥塞
基于静电场系列(ePlace series)的全局布局算法的 vanilla 优化问题为:
\[\min_{\textbf{v}}f(v)=W(\textbf{v})+\lambda D(\textbf{v}),\]其中$W(\textbf{v})$是 HPWL 的可导近似项(如 WAWL 模型),$D(\textbf{v})$是对元件进行静电场系统建模后的电势能。在静电场系统的建模中,整个版图被划分成二维格点图,每个格点称为 bin,一般来说 bin 的面积比标准单元稍大。如下图所示,RePlAce 的思路是,拉格朗日乘子$\lambda $对于每个 bin 来说是一样的,但是实际上,不同的 bin 上的密度分布是不一样的。应用一个全局的拉格朗日乘子会牺牲密度较小 bin 中的线长来减少密度较大 bin 中的密度,导致不必要的线长增加。
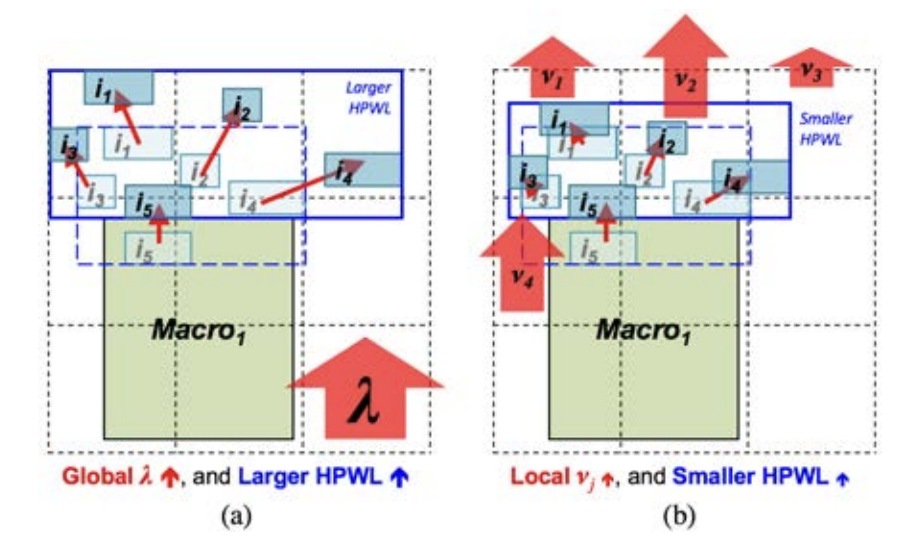
因此 RePlAce 在优化问题中加入了局部密度项$D^{local}(\textbf{v})$:
\[\min_{\textbf{v}}f(v)=W(\textbf{v})+\lambda D^{global}(\textbf{v}) + D^{local}(\textbf{v}),\]其中全局密度项$D^{global}(\textbf{v})$与 vanilla 优化问题形式中的一样。$D^{local}(\textbf{v})$定义为所有 bin 的区域电势能的加权和。
\[D^{l o c a l}(\mathbf{v})=\sum_{b_j \in B} \mathrm{v}_j D_j^{\text {local }}(\mathbf{v})=\sum_{b_j \in B} \mathrm{v}_j\left(\sum_{c_i \in b_j} A_{i j} q_i \phi_j\right),\]其中$A_{ij}$是 cell $i$和 bin $b_j$的重叠面积,$q_i$是 cell $i$的自带电荷,$\phi_j$是 bin $b_j$的电势能,$v_j$是与 bin $b_j$所在区域密度大小相关的一个权重,其定义为:
\[\boldsymbol{v}_j=e^{\alpha \cdot \text { Overflow }_j}=e^{\alpha \cdot\left(\text { BinDemand }_j-\text { BinCapacity }_j\right)}\]其中$\text { BinCapacity }_j$是 bin $j$的面积,$\text { BinDemand }_j$是与 bin $j$相交的 cell 面积。$\alpha$是一个控制参数,随着迭代的进行指数上升。
在使用 Nestrov 梯度算法优化求解时,对于 cell $i$使用一个修改过的梯度:
\[\operatorname{Cost}_i=\frac{\partial W(\mathbf{v})}{\partial x_i}+\lambda \frac{\partial D^{\text {global }}(\mathbf{v})}{\partial x_i}+\color{red}{\Delta_i} \frac{\partial D^{\text {local }}(\mathbf{v})}{\partial x_i}\]$\Delta_i$用于修改 cell $i$来自局部密度项的梯度,其值与其历史所在区域密度大小有关,其迭代公式如下,可以看到其值的大小与历史所在 bin 的 overflow 相关。
\[\Delta_i^{i t e r+1}=\Delta_i^{i t e r}+\beta \cdot \frac{\max \left(\text { Overflow }_j, 0\right)}{\sum_i A_i}\]改进之前的动态自适应步长
在 vanilla 优化问题中, 刚开始密度项的拉格朗日乘子$\lambda$较小,优化算法主要在优化线长,随着优化算法的进行,$\lambda$逐渐增大,优化算法开始逐渐分散元件。这个在之前$\lambda$ scaling 的算法如下:

每次迭代中,$\lambda$所乘的系数$cof$被控制在区间$[cof_{min}, cof_{max}]$内,此前工作 ePlace-MS 将这个区间为$[0.95, 1.05]$。 RePlAce 对这个区间的上限$cof_{max}$进行了改进。RePlAce 的想法时,当元件在改变移动方向的时候,$\lambda$的增长应该慢一些;当当元件在向最终位置移动的时候,$\lambda$的增长应该快一些。于是 RePlAce 先做了一次 trial placement 来判断这些时间点,并将整个过程分为三个阶段(下图的蓝、绿、黄三个阶段):
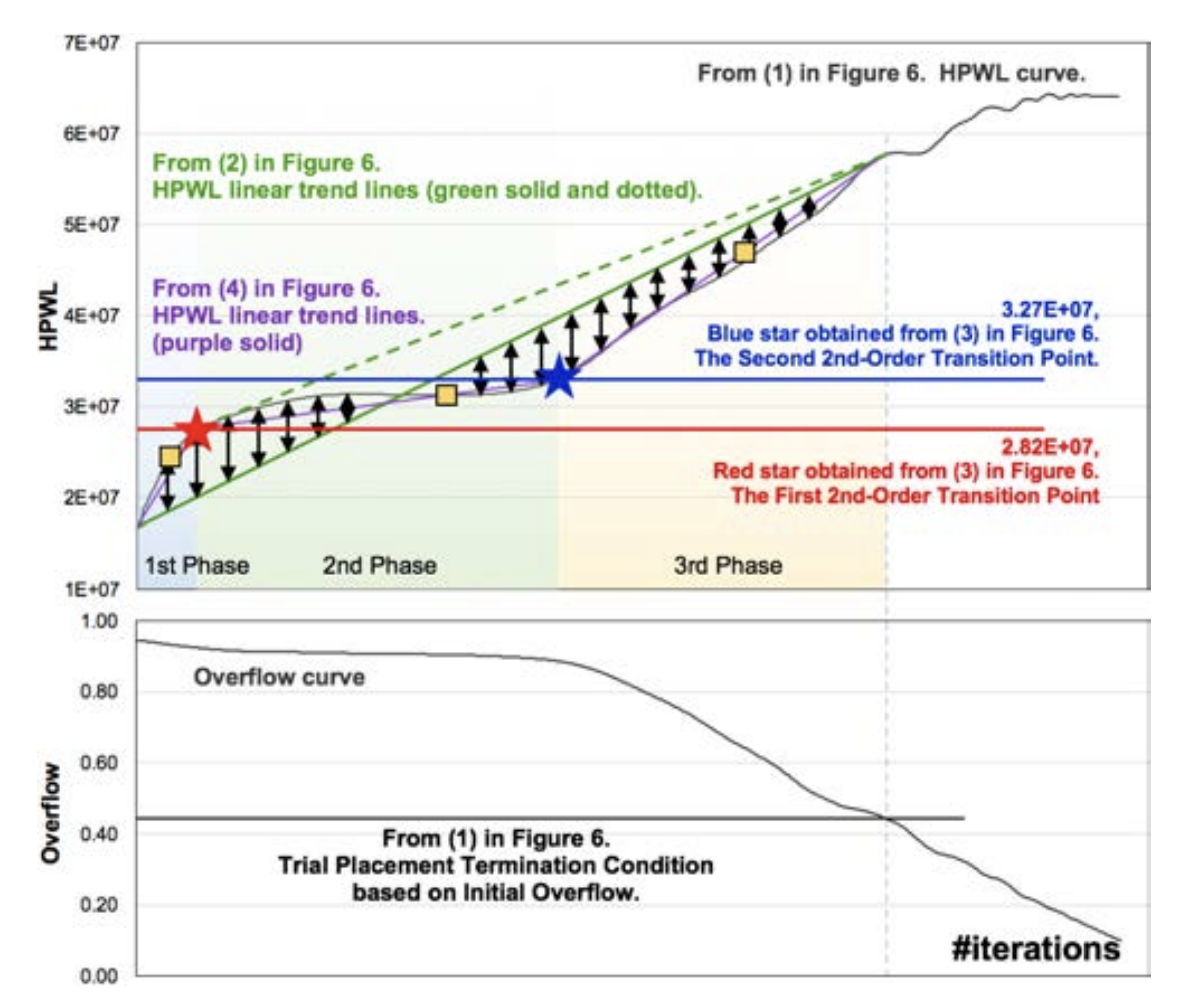
在这个图中,划分这三个阶段的是红星点和蓝星点,这两个点被称为$TP^2$点。此外在这三个阶段中各有一个黄色正方形点,这三个点被称为$TP^1$点。这两类点的判断依据是:
-
$TP^2$点是 trial placement 的 HPWL 曲线中斜率最大的两个地方。
-
$TP^2$点将整个布局过程分为三个阶段。每个阶段有一个$TP^1$点。连接各个阶段的起点和终点得到紫色线;第一个和第三阶段的$TP^1$点所在的曲线斜率与所在阶段的紫色线斜率相同;第二阶段的$TP^1$点为 HPWL 线与所在阶段的紫色线的交点。
RePlAce 认为在$TP^2$处$\lambda$增长应该较小,在在$TP^1$处$\lambda$增长应该较快,因此按照如下方式控制$cof_{max}$:
\[\operatorname{cof}_{\max}=min_{\text {cof}_{\max }}+\operatorname{cof}_{\text {range }} \times \frac{\left|H P W L_{\text {current }}-H P W L_{T P^2}\right|}{\left|H P W L_{T P^1}-H P W L_{T P^2}\right|}\]这三个阶段单独设置$\operatorname{cof}_{\max}$的在上式中的参数。实验结果表明这种设置方式在之前的$\lambda$ scaling 方法的帕累托边界之外:
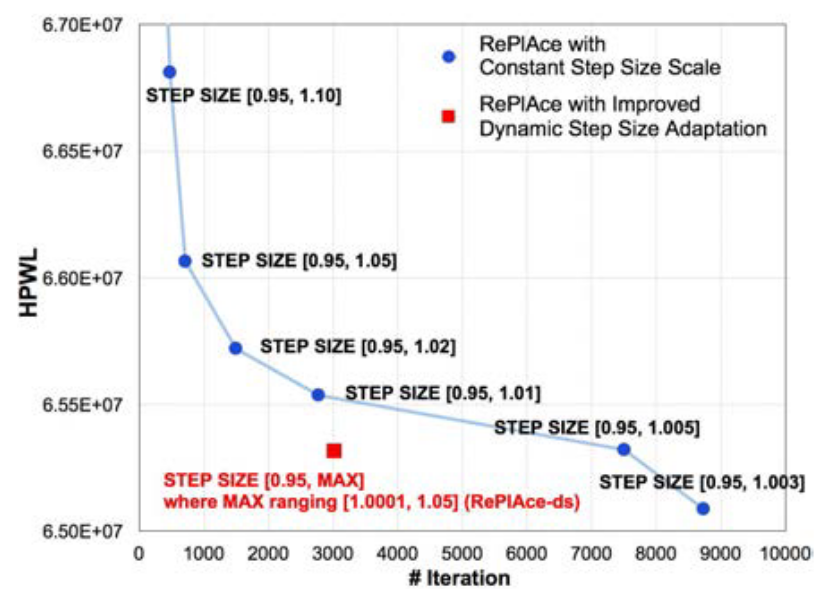
基于全局布局器 NCTU-GR 和面积放大策略的金属层感知可路由性驱动布局算法
金属层感知可路由性驱动布局算法包括四部分:layer-aware routing demand 的估计,routing blockage 的估计,routing capacity 的估计与放大系数的估计。
layer-aware routing demand 的估计
routing demand 估计的对象是每个 bin(矩形)的某条边$e$在某 metal layer $ml$的 routing demand,其公式如下:
\[\text { demand }_{e, m l}=\left(\text { usage }_{e, m l}+\gamma_{\text {pin }} \cdot \text { pincnt }\right) \cdot \text { pitch }_{m l},\]其中$\text { usage }_{e, m l}$使用$NCTU-GR$估计。此为对于 M2 及以下的层,routing 路径会被 pin 阻碍,因此对这些层还加入了 pin 的个数考虑。
routing blockage 的估计
routing demand 估计的对象与 routing demand 相同,计算方式比较简单,直接在横纵方向上数 not blocked 长度即可。
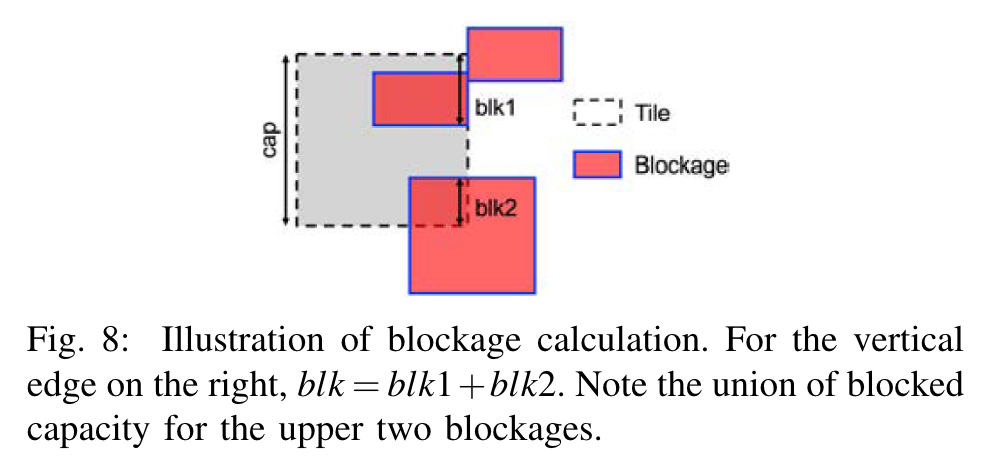
routing capacity 的估计
routing capacity 估计的对象与 routing demand 相同,这个直接从数据集获得。
放大系数的估计
放大系数估计的对象是 cell,通过计算所在 bin 的 routing demand,routing blockage 和 routing capacity 得到:
\[\text{infl ratio}=\max _{\text {all } e, m l}\left(\left(\frac{\text { demand }_{e, ml}+b l k_{e, ml}}{c_{e, m}}\right)^{\gamma_{\text {super }}}, 2.5\right)\]所有 cell 的总放大面积不能太大,RePlAce 设置了一个值max_inflated_area, 定义为初始空白面积的 10%。当所有 cell 的总放大面积超过max_inflated_area时,尝试等比例缩小每个 bin 的放大系数,直到 cell 的总放大面积不超过max_inflated_area。

实验结果
作者在如下三个数据集上进行了实验:
- ISPD-2005 and ISPD-2006 benchmarks
- MMS benchmarks
- DAC-2012 and ICCAD-2012 benchmarks。
在前两个数据集上使用 HPWL 评估效果,在 DAC 2012 和 ICCAD 2012 使用 sHPWL(scaled HPWL)来评估结果,这里的 sHPWL 由数据集官方给出定义,考虑包括 HPWL 和路由拥塞程度。
除此以外,本文还根据使用优化技术的组合提出了 RePlAce 的四个变体:
-
RePlAce-ld: 使用局部密度项; -
RePlAce-ds: 使用动态自适应步长; -
RePlAce-ldds: 使用局部密度项和动态自适应步长; -
RePlAce-r: 使用全局布局器 NCTU-GR 获得更加准确的路由估计。 -
RePlAce-r alt: 使用了 routability-driven 的NTUPlace4h作为 detailed placer(原本是使用 NTUPlace3)。
根据各个 benchmark 上是否具有 macro/是否具有路由信息,数据集和变体的组合关系如下:
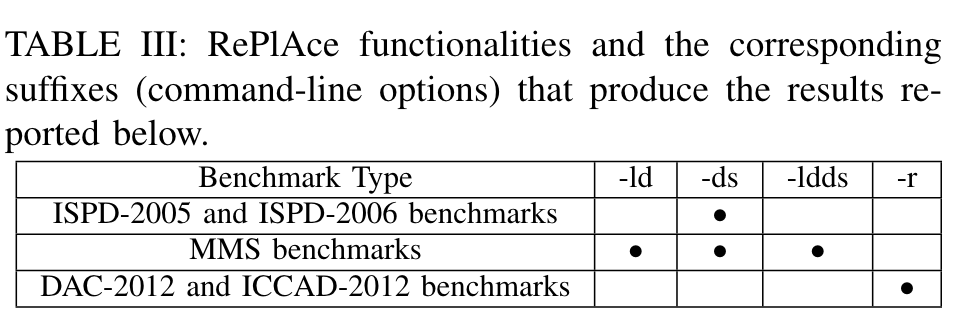
ISPD-2005, ISPD-2006 and MMS benchmarks
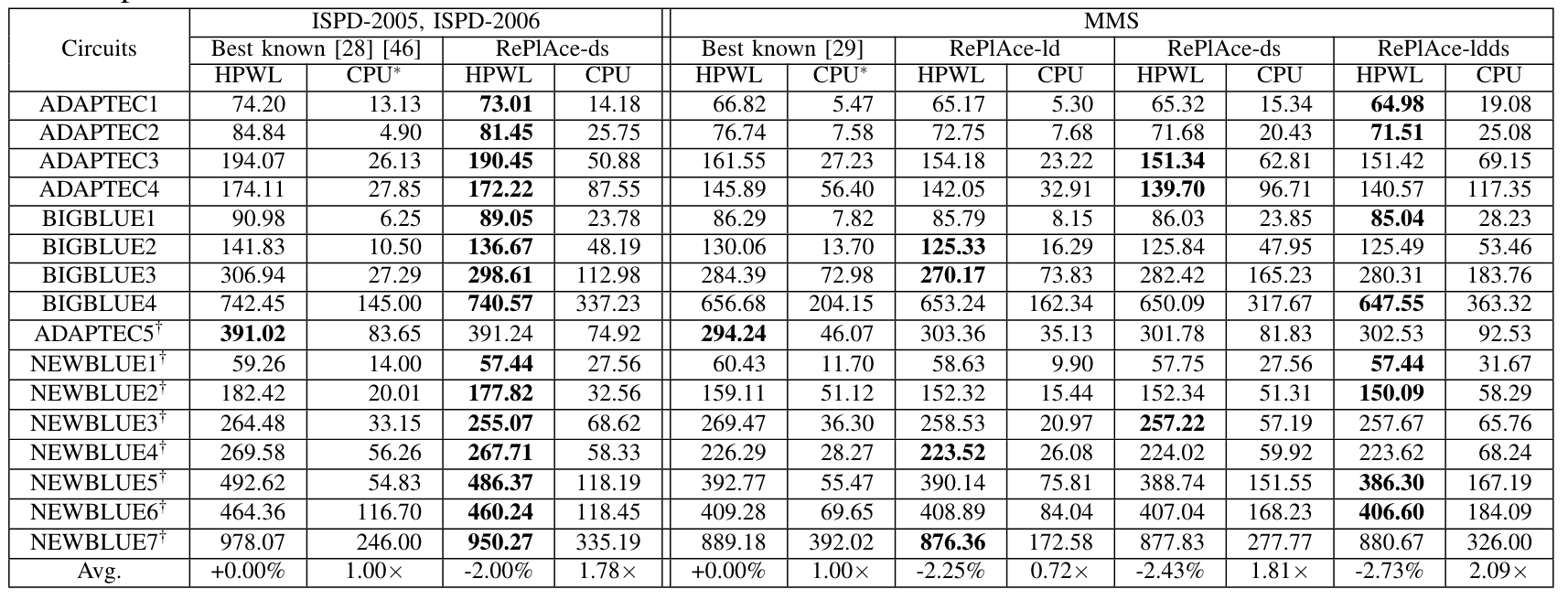
DAC-2012 benchmarks
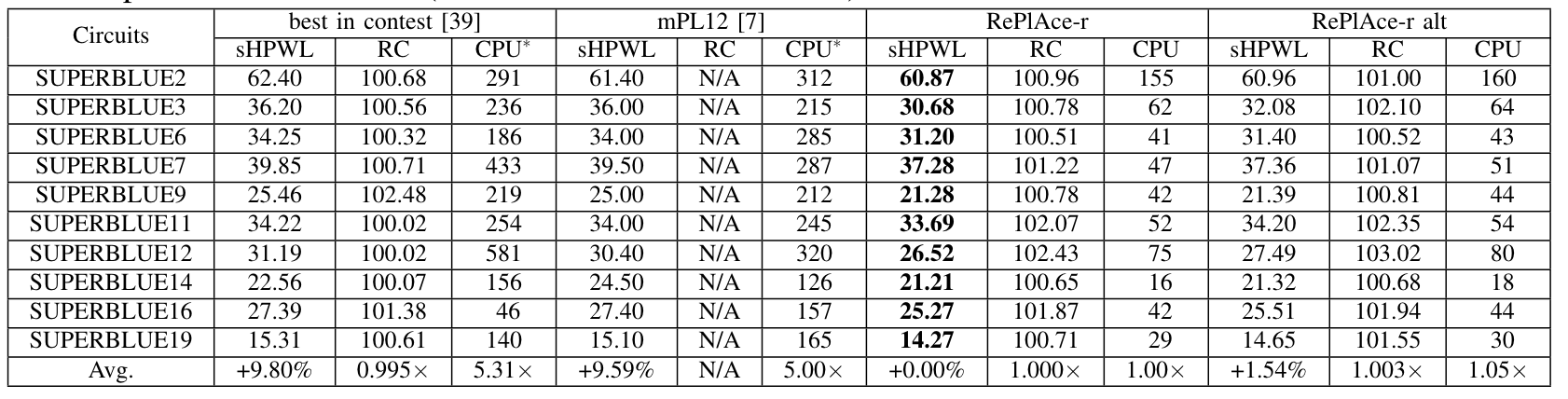
这里的实验结果表明,使用了 routability-driven detailed placerNTUPlace4h的RePlAce-r alt, 结果反而变差了。
ICCAD-2012 benchmarks
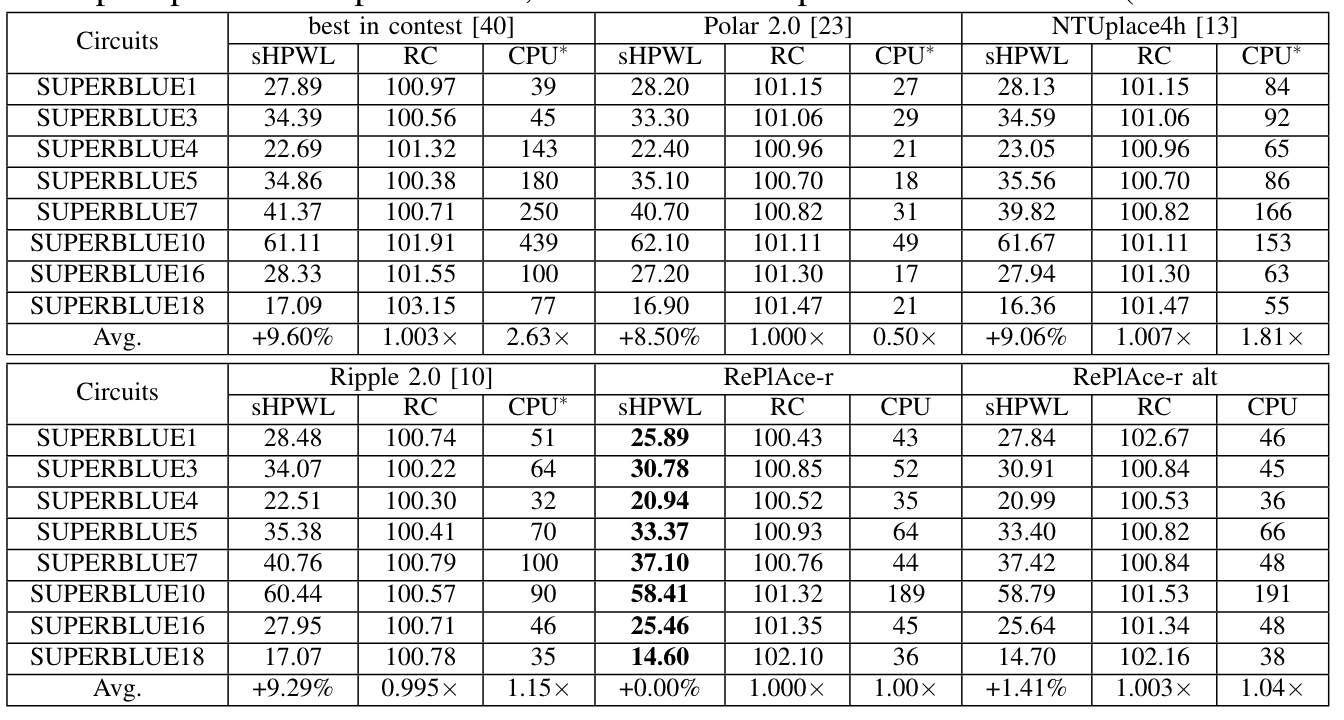
Industry benchmarks
在 JPEG, VGA, LEON3MP 和 NETCARD 四个 benchmark 上进行了实验。在相同 DRV 数量(<100)的情况下,RePlAce 平均减少了 2.4%的路由现场,并且与商业布局布线工具相比,其运行时间不到其 2 倍。
Runtime breakdown of tGP, mGP 和 cGP